Creating the Friction Surface

To set parameters for a least cost path model, we have to create a friction surface or a cost surface. Such a surface represents the cost or the friction associated with moving across each cell.

Incorporating Slope

A simple friction surface would incorporate slope. We can simply run the Least Cost Path tool with a slope surface rather than a Euclidean distance surface:

We could also rank slopes on a scale from 1 to 10 using the Reclassify tool, similar to the suitability models generated in Lab 5.

Another way to incorporate slope is to model the increasing difficulty of foot travel as slope increases:

Tan("Slope in Degrees" / 57.296) / Tan(1 / 57.296)

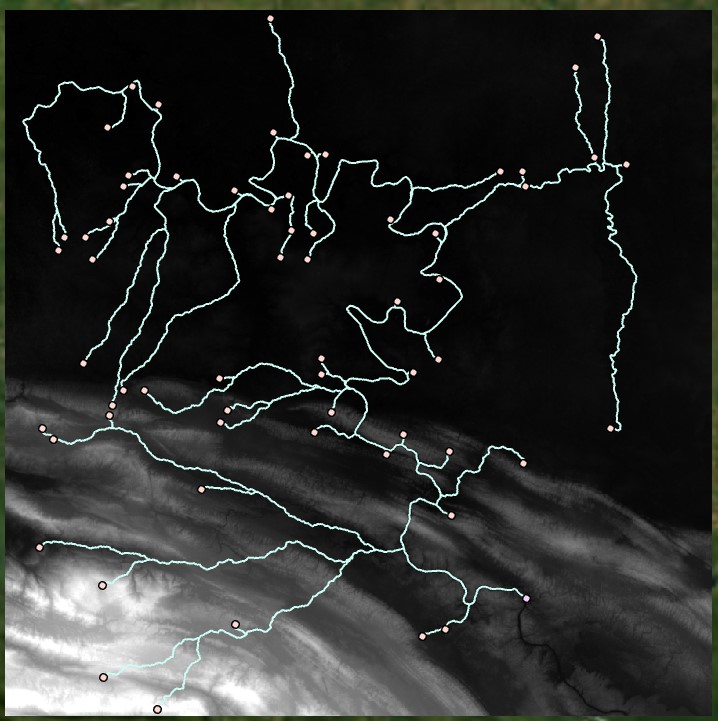
The resulting paths are similar but favor lower slopes:

We can also apply Tobler’s hiking formula, which determines the speed of an individual walking in kilometers per hour based on slope. The relationship between cost and velocity is indirectly proportional. We do not want to assign cells the value of velocity (kilometers per hour), rather we want to assign cells the time (hours per kilometer, and more appropriately hours per meter).

To apply such an analysis, we need to make sure our DEM is in a projected, metric system (UTM), using the Project Raster tool. Then, we run the following operation in Raster Calculator:

1 / (6 *  Exp(-3.5 * (Abs(Tan(("Slope Degrees") / 57.29578) + .05)))) * 3600 / 1000

This operation takes the reciprocal of the Tobler hiking algorithm and converts to seconds per meter to assign each cell a travel time in seconds per meter. Note that if we wanted each cell to represent the travel time, we would multiply by the cell size in meters. However, ArcGIS Pro tools already take cell size into account when running least cost tools. We then get the following Least Cost Paths:

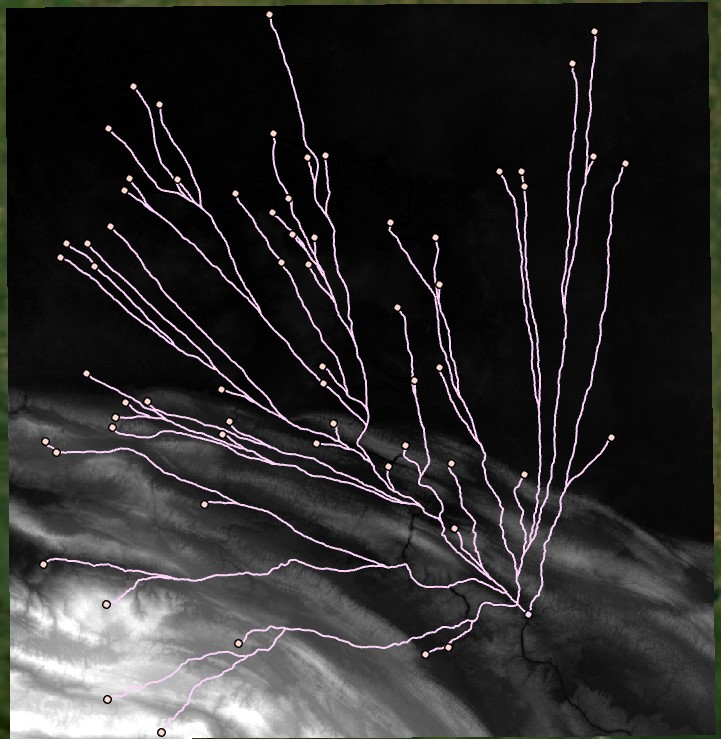
We can also generate a cost radius around a site, showing the 8-hour travel time based on the Tobler hiking formula. We can run the Distance Accumulation tool with our input cost raster output from the Tobler formula.

Incorporating Aspect

To conduct an anisotropic analysis, we have to take aspect into account. If ranking slope on a scale from 1 to 10, we could generate an Aspect surface using the Aspect tool, and use Raster Calculator to assign a weight factor when moving in the relevant uphill direction.

Alternatively, we could use the Tobler hiking formula but include negative slope values. We can generate an adjusted slope surface with the following formula:

ATan(Tan("Slope Degrees" / 57.29578) * 100 * Cos((Back Direction of Travel - "Aspect") / 57.29578) / 100) * 57.29578

Where we input the slope in degrees and the aspect, as well as specifying a back direction of travel or the direction toward the starting point (the latter can be an average direction), we get a raster of negative and positive slope values that is reminiscent of a hillshade:

Instead of inputting an average back direction, we could generate an Output Back Direction Raster using the Distance Accumulation tool (this can be based on Euclidean Distance), to generate a surface of direction toward the starting point. If the opposite direction of travel is needed, this can be calculated using a conditional statement in Raster Calculator:

Con(("Back Direction" + 180)  >=  360, "Back Direction" + 180 - 360,  "Back Direction" + 180)

When this raster is input to the Tobler hiking formula in place of the slope raster, then used to create least cost paths, we get the following:

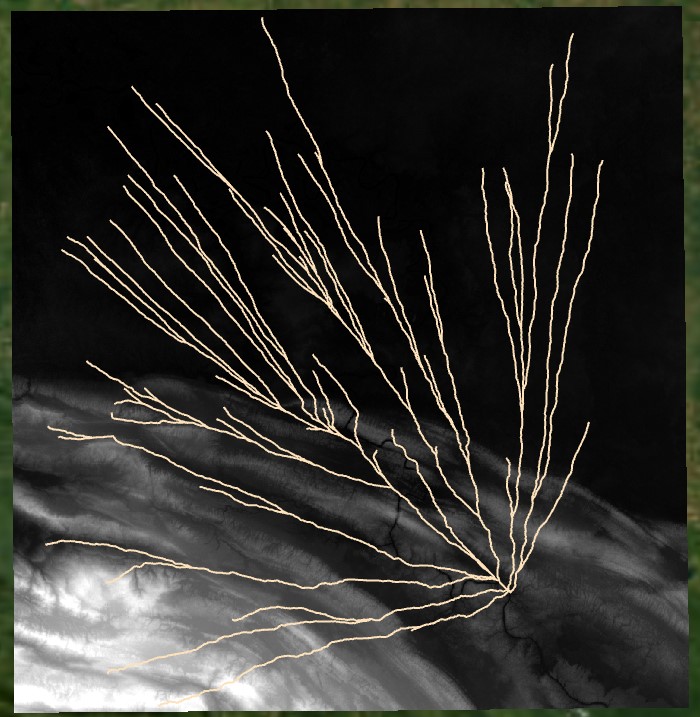
Incorporating Barriers

We can also incorporate barriers into a least cost analysis, by setting parameters that cannot be crossed. These values can be set to NoData and will be avoided when generating least cost paths. This approach is common to avoid crossing water sources. For example, we might want to walk around lakes but still cross streams. We would assign lakes a value of NoData and streams a high cost to ensure they are only crossed when necessary. Our current Tobler surface, however, has very high values for extremely steep slopes. We can also eliminate those values (by using a Set Null operation). In the following friction surface, we have retained our Tobler surface, but we have set cells above 30 seconds per meter to NoData, and we have brought in a lake layer set to NoData, as well as a stream layer set to 100. All of these datasets can be assembled using conditional statements in Raster Calculator.

We can then generate least cost paths that avoid steep slopes, lakes, and rivers: